背景

最近在研究自动化代码审计相关的东西，搜集资料时看到了南京大学的《静态软件分析》课程，理论加落地实践都有，甚至那个李老师自己还做了落地项目tai-e，现阶段还没跟完老师的课程，先暂时记录下souffle相关的笔记，后续会慢慢记录理论方面的笔记；

之前尝试过基于JVM栈结构的静态代码分析（GadgetInspector），虽然可以分析闭源软件是一个优势，但是它还是存在很多边界，而且不是很好解决；跟了李老师的课后，知道了一种更加适合静态代码分析的IR（Intermediate Representation）：3AC（3 Address Code，三地址码），原来有更好的方式早就在学术界应用已久，同时也看到了一个开源项目BytecodeDL，正是应用了这些东西进行挖洞实践！现在就是想赶快跟完老师的课程，然后看下BytecodeDL是如何落地的，然后开启疯狂的自动化漏洞挖掘之路~~~嘿嘿嘿

参考链接

Datalog语法

Datalog主要用于描述关系，是一种声明式逻辑编程语言，目前最常见的一种实现Souffle：https://souffle-lang.github.io/

谓词（Predicate/Relation）

本质上，谓词是一个数据表;
一个Fact代表一个特定的元组（也就是数据表的某一行）属于某一个Relation（也就是某一个表），即它代表一个谓词对于特定的值组合为真；

例如如下表中，Age就是一个谓词，从而得出 Age(”C0m3ct”,3) 是真，而 Age(”P1n93r”,6) 为假；

谓词：Age
person	age
C0m3ct	3
P1n93r	18

原子（Atom）

主要分为两种原子：关系型原子（Relational atom）和算术型原子（arithmetic atom）；
例如 Age(”C0m3ct”,3) 就是一个关系型原子，而 age>18 则是一个算术型原子；

规则（Rule）

Rule是逻辑表达式推理的一种方式；
Rule还用于指定如何推断事实；
Rule的格式为： H``:- B1,B2,…,Bn. ，注意最后有一个点；这个Rule表明，如果H为真，则 B1,B2,…,Bn 也必须为真；

例如通过前面的 Age(person,age) 可以推导出 Audit(person)``:- Age(person,age),age >= 18.

逻辑（Logic）

逗号表示逻辑与；
封号表示逻辑或；

最后，Header相同的多条Rule，也能表示逻辑或，例如：

1
2
Audit(person) :- Age(person,age),age > 18.
Audit(person) :- Age(person,age),age = 18.

安装Souffle

我是mac系统，直接brew安装：

1
brew install --HEAD souffle-lang/souffle/souffle

Untitled

Souffle的一个简单例子

例如如下 example.dl 文件内容：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
// 声明一个Predicate edge
.decl edge(x:number, y:number)
// 表明需要从磁盘中读取一个edge.facts文件，这里是从文件中读取facts，也可以直接在本dl中定义facts
.input edge

// 声明一个Predicate path
.decl path(x:number, y:number)
// 表明运行结束会生成一个path.facts文件
.output path

// rule推导
path(x, y) :- edge(x, y).
path(x, y) :- path(x, z), edge(z, y).

然后创建一个 edge.facts 文件，内容如下，这个就表明了edge这个Relation：

然后直接运行如下命令，得到推导出来的path结果，其中， -F 指定了facts所在的目录，而 -D 制定了输出目录， example.dl 为datalog文件：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
P1n93r@bogon example % ll
total 16
drwxr-xr-x  4 P1n93r  staff   128B  4 28 19:20 .
drwxr-xr-x  3 P1n93r  staff    96B  4 28 19:15 ..
-rw-r--r--  1 P1n93r  staff     8B  4 28 19:20 edge.facts
-rw-r--r--  1 P1n93r  staff   336B  4 28 19:19 example.dl
P1n93r@bogon example % **souffle -F. -D. example.dl**
P1n93r@bogon example % ll
total 24
drwxr-xr-x  5 P1n93r  staff   160B  4 28 19:20 .
drwxr-xr-x  3 P1n93r  staff    96B  4 28 19:15 ..
-rw-r--r--  1 P1n93r  staff     8B  4 28 19:20 edge.facts
-rw-r--r--  1 P1n93r  staff   336B  4 28 19:19 example.dl
-rw-r--r--  1 P1n93r  staff    12B  4 28 19:20 **path.csv**
P1n93r@bogon example % cat path.csv 
1	2
1	3
2	3

此外，还可以使用 -r 选项生成debug报告：

1
2
3
P1n93r@bogon example % **souffle -F. -D. -rexample.html example.dl**
P1n93r@bogon example % ll example.html 
-rw-r--r--@ 1 P1n93r  staff    76K  4 28 19:29 example.html

也可以使用 -p 选项生成分析日志，然后使用 souffleprof 进行查看：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
P1n93r@bogon example % souffle -F. -D. -pexample.log example.dl
P1n93r@bogon example % souffleprof example.log                 
SouffleProf
    runtime  loadtime  savetime relations     rules    tuples generated
      .000s     .000s     .000s         2         4             5

Slowest relations to fully evaluate
 ----- Relation Table -----
   TOT_T  NREC_T   REC_T  COPY_T  LOAD_T  SAVE_T  TUPLES   READS   TUP/s    ID NAME

   .000s   .000s   .000s   .000s   .000s   .000s       3       1   20.0K    R2 path
   .000s   .000s   .000s   .000s   .000s   .000s       2       0       2    R1 edge

Slowest rules to fully evaluate
  ----- Rule Table -----
   TOT_T  NREC_T   REC_T  TUPLES   TUP/s      ID RELATION

   .000s   .000s   .000s       1 55.5556    C2.1 path
   .000s   .000s   .000s       2 166.667    N2.1 path

  cpu total
      .009s
   211%         
   190%       * 
   169%       * 
   148%       * 
   126%       * 
   105%       * 
    84%  *******
    63%  *******
    42%  *******
    21%  *******
        --------

> rel 
 ----- Relation Table -----
   TOT_T  NREC_T   REC_T  COPY_T  LOAD_T  SAVE_T  TUPLES   READS   TUP/s    ID NAME

   .000s   .000s   .000s   .000s   .000s   .000s       3       1   20.0K    R2 path
   .000s   .000s   .000s   .000s   .000s   .000s       2       0       2    R1 edge

First Example

传递闭包分析示例（Transitive clousure）

集合 X 上的关系 R 是可传递的，如果对于 X 中的所有 x、y、z，只要 x R y 和 y R z 则 x R z。在下面的示例中，我们考虑一个有向图，其中 edge 定义关系，如果满足下面的两个 rule 之一，则元组位于传递闭包（可达关系，reachable relation）中。

1
2
3
4
5
6
7
8
9
.decl edge(n: symbol, m: symbol)
edge("a", "b"). /* facts of edge */
edge("b", "c").
edge("c", "b").
edge("c", "d").
.decl reachable (n: symbol, m: symbol)
.output reachable // output relation reachable
reachable(x, y):- edge(x, y). // base rule
reachable(x, z):- edge(x, y), reachable(y, z). // inductive rule

运行结果如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
P1n93r@bogon example % souffle -F . -D . test.dl 
P1n93r@bogon example % ll
total 16
drwxr-xr-x  4 P1n93r  staff   128B  4 29 10:36 .
drwxr-xr-x  4 P1n93r  staff   128B  4 28 19:33 ..
-rw-r--r--  1 P1n93r  staff    36B  4 29 10:36 reachable.csv
-rw-r--r--  1 P1n93r  staff   312B  4 29 10:35 test.dl
P1n93r@bogon example % cat reachable.csv 
a	b
a	c
a	d
b	b
b	c
b	d
c	b
c	c
c	d

同代分析示例（Same generation example）

给定一棵树（具有特定根节点的非循环有向图），目标是找出哪些节点位于同一级别（同代）。

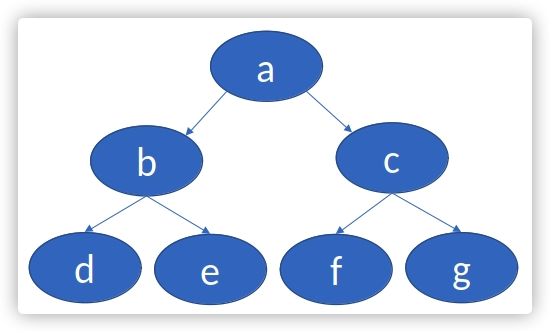
Untitled

可以很直观的看到，节点 b 和 c 是同代， e 和 g 也是如此；使用datalog解决这个问题，可以编写如下dl（解释在注释中了）：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
// 定义一个谓词，用于描述 子-父 关系
.decl Parent(n: symbol, m: symbol)

// Parent谓词的一系列事实（Facts）
Parent("d", "b"). Parent("e", "b"). Parent("f","c").
Parent("g", "c"). Parent("b", "a"). Parent("c","a").

// 定义一个谓词，用于描述单个节点
.decl Node(n: symbol)
Node(x) :- Parent(x, _).
Node(x) :- Parent(_, x).

// 定义一个谓词，用于描述同代关系
.decl SameGeneration (n: symbol, m: symbol)

// 定义两条rule
// 对于某个节点，自己和自己是同代
SameGeneration(x, x):- Node(x).
// 如果两个子节点的父节点是同代，那么这两个子节点是同代
SameGeneration(x, y):- Parent(x,p), SameGeneration(p,q), Parent(y,q).
.output SameGeneration

运行结果如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
P1n93r@bogon example % souffle -F . -D . test.dl
P1n93r@bogon example % ll
total 16
drwxr-xr-x  4 P1n93r  staff   128B  4 29 11:00 .
drwxr-xr-x  4 P1n93r  staff   128B  4 28 19:33 ..
-rw-r--r--  1 P1n93r  staff    84B  4 29 11:00 SameGeneration.csv
-rw-r--r--  1 P1n93r  staff   732B  4 29 11:00 test.dl
P1n93r@bogon example % cat SameGeneration.csv 
d	d
d	e
d	f
d	g
b	b
b	c
e	d
e	e
e	f
e	g
f	d
f	e
f	f
f	g
c	b
c	c
g	d
g	e
g	f
g	g
a	a

数据流分析示例

数据流分析 (DFA，Data Flow Analysis) 旨在确定程序的静态属性。 DFA 是一个统一的理论，为程序的全局分析提供信息。 DFA 基于控制流图 (CFG，Control Flow Graph)，其中程序的分析源自节点和图的属性。

数据流分析中最简单的就是定值可达分析（Reaching Definition Analysis），对于数据流分析的理论知识，可以通过南大《静态软件分析》课程进行学习，这里是课程PPT：https://pascal-group.bitbucket.io/teaching.html

我这里简单说明下定值可达分析的基本概念：

如果v在p点有定值d，存在一条从p到q的路径，在这个路径上没有其他的定值点，则称v的定值d到达（reaching）p；
如果从p到q的路径上有其他对于v的定值，我们就说v的定值d被kill掉了；

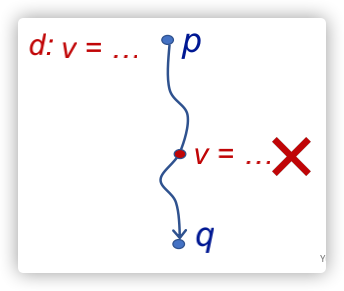
Untitled

例如如下的CFG（控制流图）：

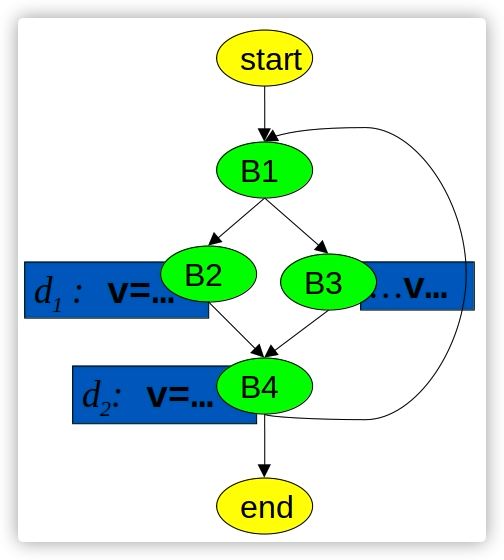
Untitled

此时我们可以编写如下dl进行定值可达分析：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// define control flow graph
// via the Edge relation
.decl Edge(n: symbol, m: symbol)
Edge("start", "b1").
Edge("b1", "b2").
Edge("b1", "b3").
Edge("b2", "b4").
Edge("b3", "b4").
Edge("b4", "b1").
Edge("b4", "end").

// Generating Definitions
.decl GenDef(n: symbol, d:symbol)
GenDef("b2", "d1").
GenDef("b4", "d2").

// Killing Definitions
.decl KillDef(n: symbol, d:symbol)
KillDef("b4", "d1").
KillDef("b2", "d2").

// Reachable
.decl Reachable(n: symbol, d:symbol)
// gen点意味着当前定值一定可达gen点
Reachable(u,d) :- GenDef(u,d).
// 这个地方souffle官方写的是：Reachable(v,d) :- Edge(u,v), Reachable(u,d), !KillDef(u,d).
// 我认为souffle官方应该是写错了，从逻辑上来讲，定值可达u点，并且在v点不被kill掉，才能说定值可到v
// 如果是souffle官方的写法，那么逻辑就是：定值可达u点，且在u点定值不被kill掉，就说明u点可达v点，感觉是不符合定值可达分析的定义的
Reachable(v,d) :- Edge(u,v), Reachable(u,d), !KillDef(v,d).

.output Reachable

输出结果如下（如果用souffle官方给的dl，得出的结果中，还存在定值d1可达B4，显然是错误的）：

1
2
3
4
5
6
7
P1n93r@bogon example % souffle -F . -D . test.dl
P1n93r@bogon example % cat Reachable.csv 
b1	d2
b2	d1
b3	d2
b4	d2
end	d2

一些备注

souffle支持两种注释：

1
2
// 这里是注释
/* 这里也是注释 */

souffle支持C预处理器（比如定义宏），例如：

1
2
#include "myprog.dl"
#define MYPLUS(a,b) (a+b)

关系（Relations）

关系声明

关系的声明有点类似前面说到的datalog的谓词，用于定义一系列特定的元组存在的某种关系，例如如下的关系定义/声明：

1
2
// 定义了一个关系edge，代表一系列特定元组 (a, b) 存在edge这个关系，a和b的类型都是symbol，这是一种类似strings的类型
.decl edge(a:symbol, b:symbol)

I/O指令

编写dl文件的时候，我们可以使用IO指令进行fact的加载和输出，前面的案例中也用到了，这些指令分别为：

.input <relation-name> 指令：从 <relation-name>.facts 中加载facts，默认使用tab进行数据分隔；
.out <relation-name> 指令：默认情况下，将分析得出的facts写出到 <relation-name>.csv 文件中；
.printsize <relation-name> 指令：在控制台中打印给定关系的facts数量；

语法糖

为了减少代码编写工作量，可以使用在规则中编写多个head，如下所示，左边是使用了语法糖的情况，右边是没有使用语法糖的情况：

Untitled

类似的，也可以在规则体中使用析取（disjunction），如下所示，左边是使用了语法糖的情况，右边是没有使用语法糖的情况（规则推导中的封号代表逻辑或）：

Untitled

属性的类型（Type system for attributes）

souffle的类型是静态的，必须在编译之前确定关系（relation）的属性，并在编译时进行类型检查；

原始类型

souffle存在两种原始类型：

symbol：它包含所有的字符串，它的内部实现是一个ordinal number；
number：和 int 类似；

算术表达式

souffle支持算术函子（arithmetic functors），扩展了传统的datalog语义；函子中使用的变量必须要能终止，也就是意味着函子中使用的变量不能是无限的，一个例子如下，使用了算术运算符 < ：

1
2
3
4
.decl A(n: number)
.output A
A(1).
A(x+1) :- A(x), x < 9.

souffle支持的算术函子如下：

加法：x+y ；
减法：x-y ；
除法：x/y ；
乘法：x*y ；
模数：a%b ；
幂运算：a^b ；
计数器：autonic() ；
位操作：x band y 、 x bor y 、 x bxor y 和 bnot x ；
逻辑操作：x land y 、 x lor y 和 lnot x ；

souffle支持如下算术约束：

小于：a < b ；
小于或等于：a <= b ；
等于：a = b ；
不等于：a != b ；
大于或等于：a >= b ；
大于：a > b ；

写规则的时候，可以在源码中使用十进制、二进制和十六进制：

1
2
3
4
.decl A(x:number)
A(4711).
A(0b101).
A(0xaffe).

Notice: 在facts文件中，只支持十进制；

数字编码（Number encoding）

类似C一样，数字可以用于逻辑运算：

0代表false；
非0代表true；

因此，数字可用于这些逻辑运算：x land y、x lor y 和 lnot x 示例如下：

1
2
3
.decl A(x:number)
.output A
A(0 lor 1).

autonic()函子

函子 autoinc() 每次计算时都会生成一个新数字。但是，在递归关系中是不允许使用的。它可用于为符号创建唯一编号（充当标识符），例如以下示例：

1
2
3
4
5
6
.decl A(x: symbol)
A("a"). A("b"). A("c"). A("d").

.decl B(x: symbol, y: number)
.output B
B(x, autoinc()) :- A(x).

输出如下：

1
2
3
4
5
6
P1n93r@bogon example % souffle -F . -D . test.dl
P1n93r@bogon example % cat B.csv 
a	0
b	1
c	2
d	3

Aggregation（聚合）

Soufflé 中的聚合（aggregation）是指使用特定的函子来汇总有关查询的信息。聚合只能应用于 Soufflé 中的稳定关系。聚合的类型包括计数、查找一组数字的最小值/最大值以及求和。通常在 Soufflé 中，信息不能从子目标（聚合函子的参数）流向外部范围。例如，如果希望找到关系 Cost(x) 的最小值，无法找到使 Cost(x) 最小化的特定 x 值。因为实际上，这样的 x 值可能不是唯一的。

计数（Counting）

技术函子（counting functor）可以用于计算目标facts的大小，语法为： count:{<sub-goal>} ，如下就是一个计算绿色车辆个数的例子：

1
2
3
4
5
6
7
8
.decl Car(name: symbol, colour:symbol)
Car("Audi", "blue").
Car("VW", "red").
Car("BMW", "blue").

.decl BlueCarCount(x: number)
BlueCarCount(c) :- c = count:{Car(_,"blue")}.
.output BlueCarCount

输出如下：

1
2
3
4
5
6
7
8
9
P1n93r@bogon example % souffle -F . -D . test.dl
P1n93r@bogon example % ll
total 16
drwxr-xr-x  4 P1n93r  staff   128B  4 29 17:21 .
drwxr-xr-x  4 P1n93r  staff   128B  4 28 19:33 ..
-rw-r--r--  1 P1n93r  staff     2B  4 29 17:21 BlueCarCount.csv
-rw-r--r--  1 P1n93r  staff   196B  4 29 17:21 test.dl
P1n93r@bogon example % cat BlueCarCount.csv 
2

求最大/最小/和

求最大值的算术语法为：max <var>:{<sub-goal(<var>)>} ，例子如下：

1
2
3
4
5
.decl A(n:number)
A(1). A(10). A(100).
.decl MaxA(x: number)
MaxA(y) :- y = max x:{A(x)}.
.output MaxA

求最小值和总和语法也是类似：

求最小值：min <var>:{<sub-goal(<var>)>} ；
求和： sum <var>:{<sub-goal(<var>)>} ；

记录（Records）

关系（Relation）是 Datalog 中的二维结构。对于大型代码库和/或复杂问题，可以方便地考虑具有更复杂结构（递归/层次结构等）的关系。由于调用记录（Record）时需要额外的表查找，所以记录提供了这样的抽象，并且以性能为代价打破了 Datalog 的扁平世界。它们的语义与 Pascal/C 中的语义相当。将来，记录的联合将被允许模拟多态性。记录类型定义的语法如下：

1
.type <name> = [ <name_1>: <type_1>, ..., <name_k>: <type_k> ]

一个例子如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
// Pair of numbers
.type Pair = [a:number, b:number]

.decl A(p: Pair)  // declare a set of pairs
A([1,2]).
A([3,4]).
A([4,5]).

.decl Flatten(a:number, b:number)
.output Flatten
Flatten(a,b) :- A([a,b]).

记录的内部结构（Overview of record internals）

每个记录类型都有一个隐藏的类型关系。在这个隐藏的关系中，记录的元素被转换为数字。在计算期间，如果记录不存在，则会即时创建。一个例子如下：

1
2
3
4
5
.type Pair = [a: number, b: number]
.decl A(p: Pair)
A([1,2]).
A([3,4]).
A([4,5]).

对于这个这个例子，记录的内部结构如下：

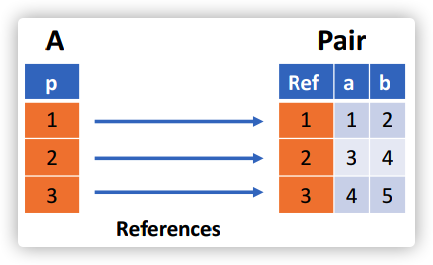
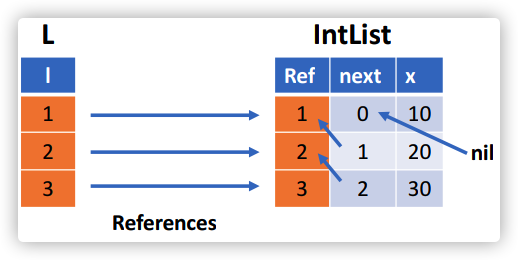
Untitled

递归记录（Recursive records）

Soufflé 中允许递归定义的记录。递归因 nil 记录的存在而终止。例如如下例子(souffle官方的又写错了)：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
.type IntList = [next: IntList, x: number]
.decl L(l: IntList)

L([nil,10]).

// [r1,x+10] 代表需要推导的下一个IntList，其中r1代表上一个IntList，r2也是代表需要推导出的下一个IntList（独立于[r1,x+10]），这个需要推导出来的r2需要满足[r1, x],也就是next为r1（上一个IntList）
L([r1,x+10]) :- L(r2), r2=[r1,x], x < 30.
.decl Flatten(x: number)
Flatten(x) :- L([_,x]).
.output Flatten

运行结果如下：

1
2
3
4
5
P1n93r@bogon example % souffle -F . -D . test.dl
P1n93r@bogon example % cat Flatten.csv          
10
20
30

此时这个内部结构如下所示：

Untitled

Souffle学习笔记

文章目录

背景

参考链接

Datalog语法

谓词（Predicate/Relation）

原子（Atom）

规则（Rule）

逻辑（Logic）

安装Souffle

Souffle的一个简单例子

First Example

传递闭包分析示例（Transitive clousure）

同代分析示例（Same generation example）

数据流分析示例

一些备注

关系（Relations）

关系声明

I/O指令

语法糖

属性的类型（Type system for attributes）

原始类型

算术表达式

数字编码（Number encoding）

autonic()函子

Aggregation（聚合）

计数（Counting）

求最大/最小/和

记录（Records）

记录的内部结构（Overview of record internals）

递归记录（Recursive records）