Interprocedural Analysis

Motivation

到目前为止，我们学习的分析都是程序内分析（Intraprocedural），这种分析是不处理方法调用的，如果碰到了方法调用，基于Inraprocedural的分析是如何处理的呢？例如存在如下程序（常量传播，Constant Propagation）：

Untitled

Inraprocedural analysis为了safe-approximation会采用最保守的假设，也就是假设方法调用可以做任何事情，基于这种过于保守的假设，在Inraprocedural analysis下，会认为：

1
2

n = NAC
x = NAC, y = NAC

所以可以看到，如果使用Inraprocedural anlysis处理过程调用（method calls），那么就会丢失很多精度（imprecesion），为了更准确的精度，我们需要过程间分析（Interprocedural analysis），过程间分析会沿着过程间的控制流edges进行数据流传播，使用过程间分析，对于上面的常量传播实例程序，可以得到：

1
2

x = 42, y = 43
n = 10

所谓过程间的控制流edges的图示如下：

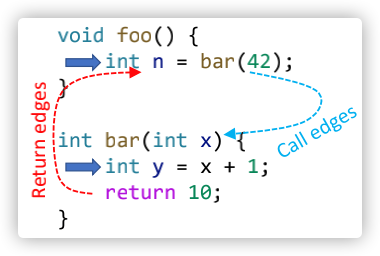
Untitled

同时，为了更好的过程间分析，我们需要call graph；

Call Graph Construction(CHA)

call graph的定义：call graph即为程序中调用关系的表示，本质上，call graph是一组从call-sites到他们的目标方法的调用边（call edges），call-sites的目标方法称为（callees）；

如下是call graph的图示：

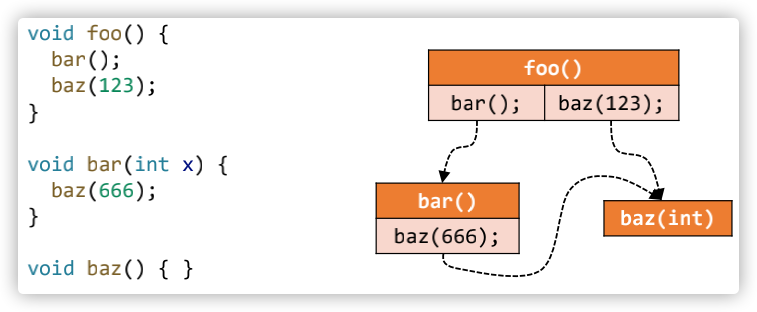
Untitled

call graph是过程间分析的基础，是非常重要的程序信息；对于调用图构建比较有代表性的集中算法如下，越往上，速度越快，但是精度越低，越往下速度越慢，但是精度越高。我们主要学习的就是CHA和k-CFA算法：

Untitled

Method Calls(Invocations) in Java

对于Java而言，其函数调用可以分析如下三种，其中Virtual Call主要应用于多态，因为多态，其目标方法只能在运行时确定；在Java中，认为除了静态方法、构造方法、私有方法和父类方法，其他的都为Virtual Call；

一个用于描述Java中的方法调用的表格如下：

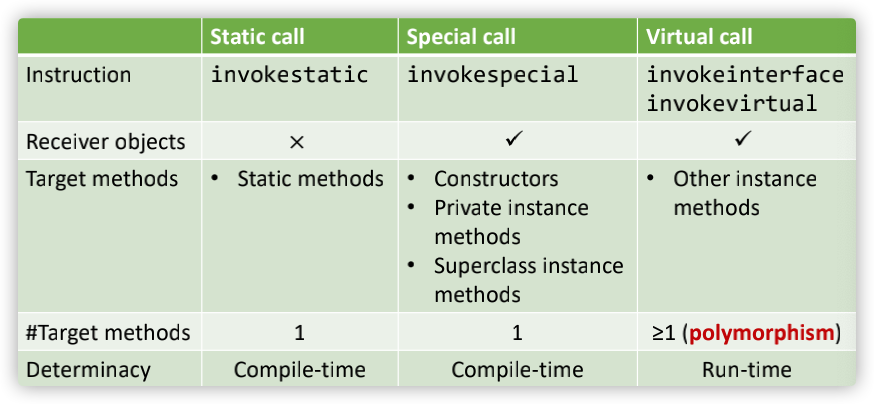
Untitled

其中的Virtual Call对于OOPLs（面向对象程序语言）的call graph construction非常关键；

Method Dispatch of Virtual Calls

在运行时，一个virtual call的解析主要取决于：

  1. receiver object的type；
  2. call site的方法签名（method signature）；

我们暂且认为方法签名由以下部分组成：

1
2

Signature = class type + method name + descriptor
Descriptor = return type + parameter types

图示如下：

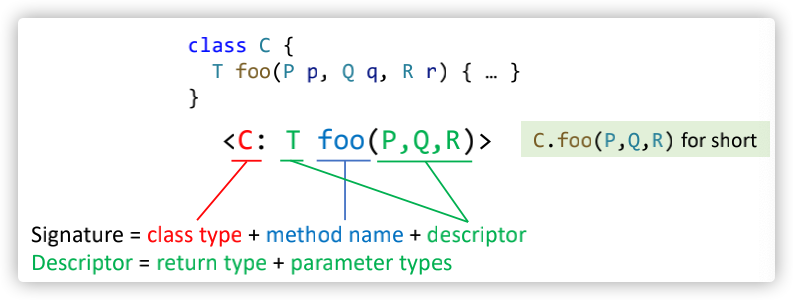
Untitled

最后我们可以定义一个 Dispatch(c, m) 方法来模拟运行时call-site具体方法的调用；算法如下：

Untitled

其中，c指的是receiver object的true type，而m指的是call site的方法的签名；对于这个Dispatch方法而言，这个call site的方法签名中，class type指的是declared type；

一个使用案例如下：

Untitled

Class Hierarchy Analysis(CHA)

  • CHA即为类层次结构分析算法，对于这种算法，它需要知道程序中类的继承结构信息（hierarchy information），例如需要知道某个类的父类和子类有哪些；
  • CHA的主要思想就是在一个call site中，根据receiver variable的desclared type计算virtual call；
  • CHA假设变量a可以指向类A以及类A的所有子类的对象，所以CHA计算目标方法的过程就是查询类A的整个继承结构来查询目标方法；
  • CHA算法是1995年在ECOOP会议上首次发表出来的；

如下是CHA的一个具体算法，其中的cs指的是call site：

Untitled

根据这个算法进行一个案例计算，图示如下：

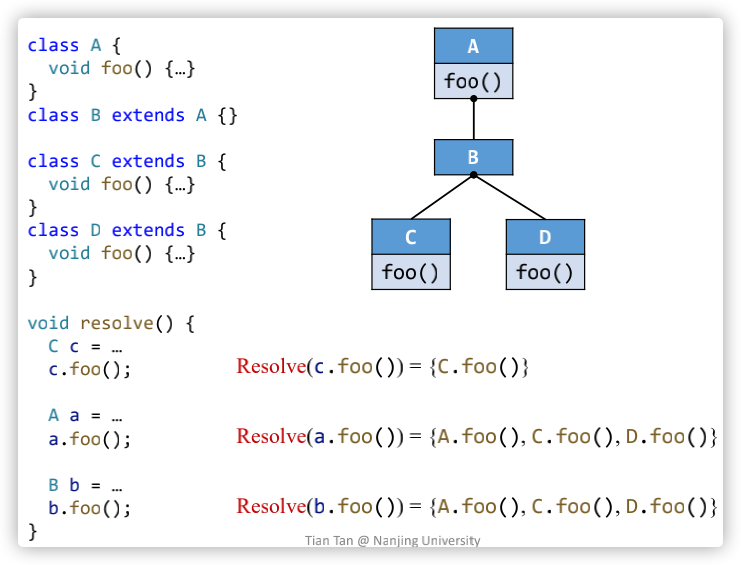
Untitled

Features of CHA

CHA的优势是速度快，原因如下：

  • 只考虑call site中receiver variable的declared type和它的继承结构；
  • 忽略数据流和控制流信息；

CHA的劣势是精度较低，原因如下：

  • 容易引入虚假目标方法；
  • 没有使用指针分析；

Call Graph Construction

通过CHA算法生成call graph的步骤如下：

  • 从入口方法开始（例如对于Java而言的main方法）；
  • 对于每一个可达方法m，在方法m中通过CHA算法为每一个call site计算目标方法；
  • 重复这个过程直到没有新的方法被发现；

图示如下所示，灰色的部分就是代表不可达的方法：

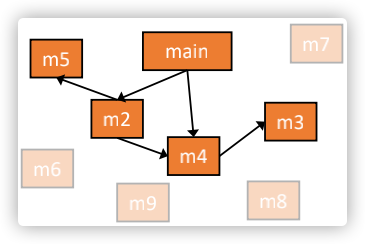
Untitled

具体的算法如下：

Untitled

一个使用CHA构建call graph的演算案例如下：

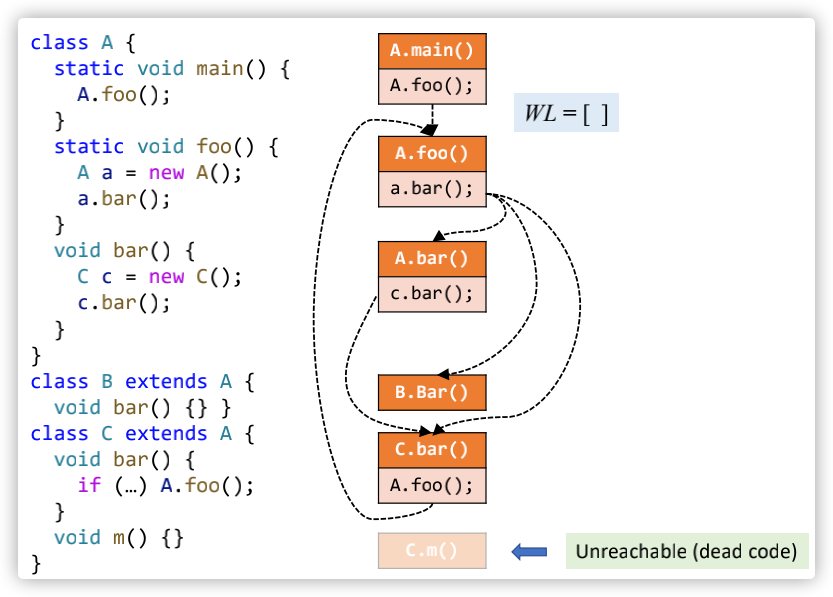
Untitled

Interprocedural Control-Flow Graph

  • CFG 表示单个方法的结构；
  • 而ICFG表示整个程序的结构，基于ICFG，我们可以进行过程间（Interprocedural）分析；
  • ICFG由程序中各个方法的CFG组成，但是还需要再多添加两条额外的边：Call edges和Return edges；
  • Call edges指的就是：从call sites指向其被调用方法（callees）内部节点的edges；
  • Return edges指的就是：从被调用方法的exit节点指向与之对应的call site紧接着的下一个statement；
  • 连接Call edges和Return edges两种类型的边的信息，来自于call graph；

总结一下，就是：

1

ICFG = CFGs + call & return edges

一个ICFG案例如下（基于值传递，非指针传递）：

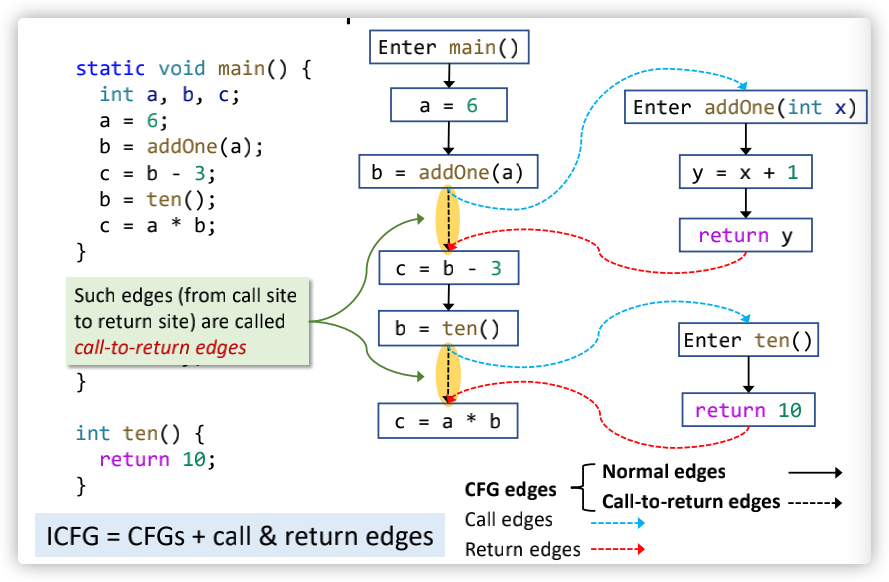
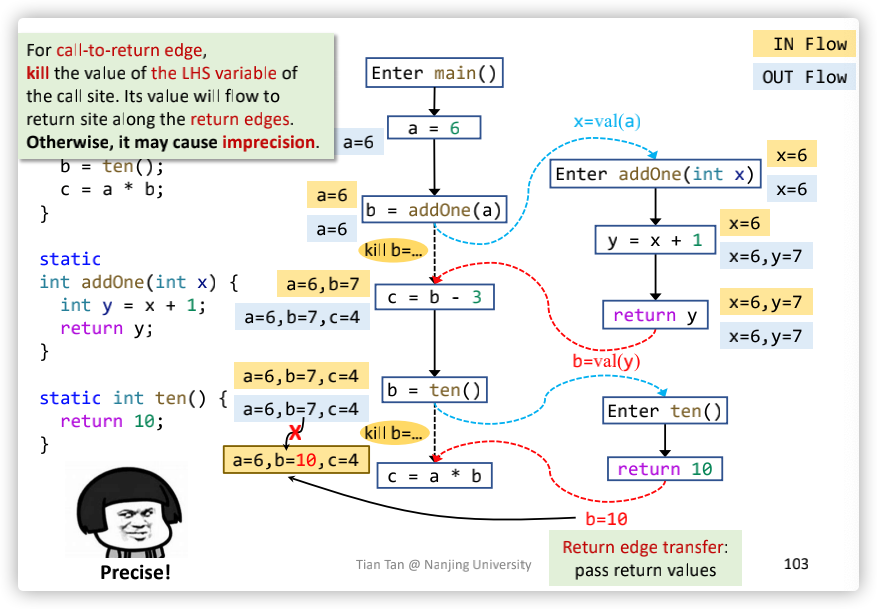
Untitled

这里需要注意黄色标记的call-to-return edge，既然数据流可以从return edge往下连接起来，为啥还需要存在call-to-return edge？因为如果不保留call-to-return edge，那么就需要在callee中维护与实参无关的数据传播；有了call-to-return edge，那么与实参无关的数据就可以通过这条边直接传递下去了，无需经过callee；

Interprocedural Data-Flow Analysis

之前我们基于CFG进行数据流分析，其transfer functions主要是node transfer，而基于ICDF（过程间控制流图，Interprocedural Control Flow Graph）进行数据流分析，其transfer functions主要是node transfer加上edge transfer；

edge transfer主要分为如下两种：

  • call edge transfer：沿着call edge，将来自于call site的数据流转换到callee中的节点；
  • return edge transfer：沿着return ege，将来自于callee的exit节点的数据流转换到return site；

Interprocedural Constant Propagation

  • Call edge transfer：传递参数值；
  • Return edge transfer：传递返回值；
  • Node transfer：和过程内的常量传播一致，但是如果是call nodes，transfer function就是一个特殊的function；

对于Interprocedural Constant Propagation的call node transfer，它会杀死这个node的左边的变量，把左边的变量的数据流处理交给edge transfer，图示如下：

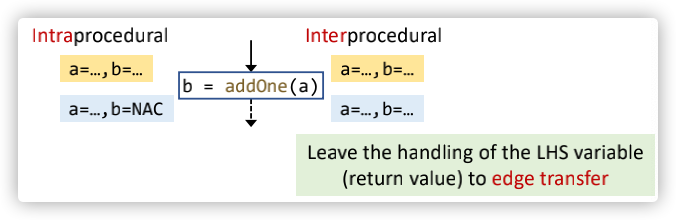
Untitled

对于call node transfer的一个更加直观的图示，画×部分代表b变量被kill了，但是后面经过return edge transfer还是把b变量传播下来了，并且没有丢失精度：

Untitled