Data_Flow_Analysis
文章目录
Data Flow Analysis
说明
时间有限,只过了一遍数据流分析中的定值可达分析和变量存活分析,有关数据流分析的Foundation部分没有跟了,后期有时间再慢慢跟一下;
Overview of Data Flow Analysis
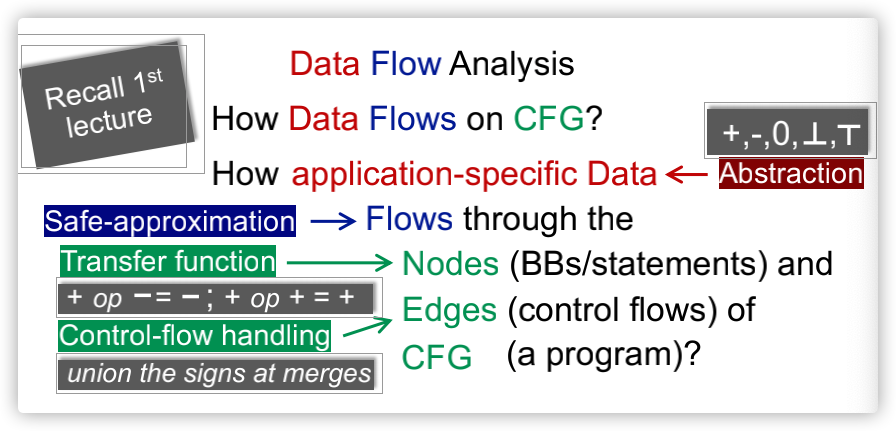
Data Flow Analysis可以概括为:How Data Flows on CFG?再详细一点,就是:How application-specific Data Flows through the Nodes(BBs/statements) and Edges(control flows) of CFG(a program)?
- 这里的application-specific Data指的就是我们静态分析时关注的抽象(Abstractiion)数据;
- Node通常通过转换函数(Transfer functions)进行分析处理;
- Edge的分析也就是Control-flow处理;
- 不同的数据流分析存在不同的抽象数据(data abstraction)、不同的safe-approximation策略、不同的tranfer functions以及不同的control-flow handings;
图示如下:
比如我们关注程序变量的正负等状态,那么此时的application-specific Data指的就是表示变量状态的一些抽象符号;Transfer functions指的就是各种加减乘除运算;Control-flow handing指的就是merges处的符号合并;
Preliminaries of Data Flow Analysis
Input and Output States
- 每一个IR的执行,都会将input state转换成output state;
- input(output) state和statement之前(之后)的program point相关;
图示如下:
- 在每个数据流分析应用中,我们在每个program point处都关联了一个data-flow value,这个数据流值代表了可以在该点观察到的所有可能程序状态的集合的抽象;
- 数据流分析就是,对于程序中的所有IN[s]和OUT[s],需要找到一个方法去解析一系列的safe-approximation约束规则;这些约束规则基于语句的语义(transfer functions)或者控制流(flows of control);
Notations for Transfer Function’s Constraints
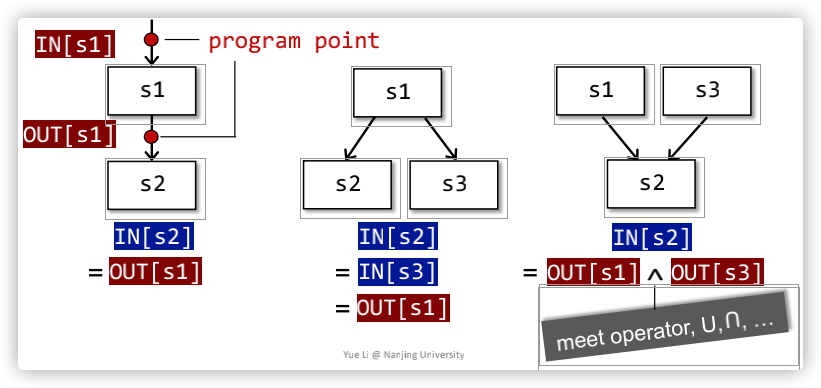
即基于转换函数的约束规则的基本概念,主要分为两种analysis,图示如下:

图示很好理解,对于Forward Analysis来讲,IN[s]经过转换函数fs的处理,可以得到OUT[s];
对于Backward Analysis来讲,OUT[s]经过转换函数fs的处理,可以得到IN[s];
Notations for Control Flow’s Constraints
即基于控制流的约束规则的基本概念,主要分为BB内和BB之间两种,图示如下:
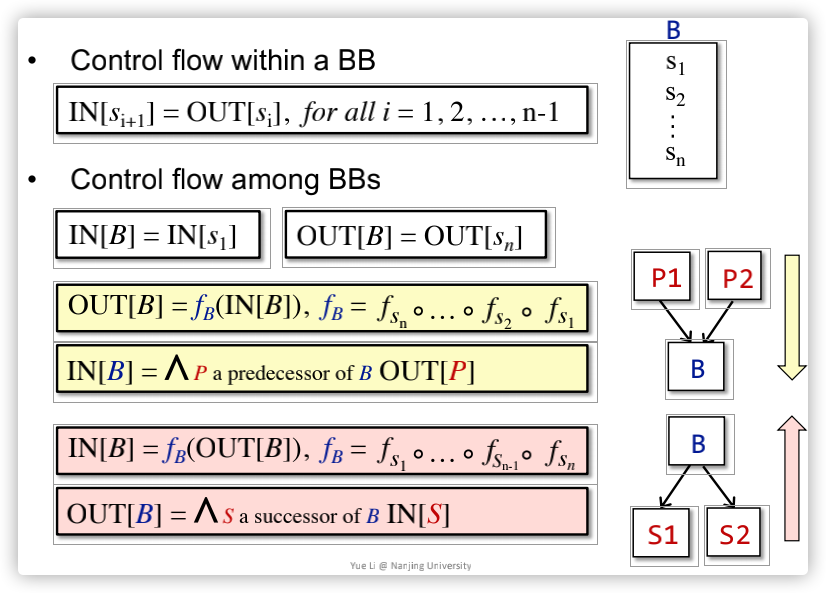
图示的一些解释如下:
- 对于
IN[Si+1] = OUT[Si],要说明的含义其实就是,对于每一个statement,后一个statement的输入就是前一个statement的输出;因为BB中的statement不能存在分叉啥的,所以能这么认为; - 对于
IN[B] = IN[S1]以及OUT[B] = OUT[Sn],要说明的含义其实就是,对于每一个BB,其输入就是第一个statement的输入,其输出就是最后一个statement的输出;
Reaching Definitions Analysis
首先解释一下可达定义分析的概念:在程序点(program point)p存在一个对v变量的定义d,且存在一条从p到q的路径,在这个路径上不存在对变量v的新的定义,此所谓定义可达;如果在这个路径上存在对变量v的新的定义,则称定义d被killed;图示如下:
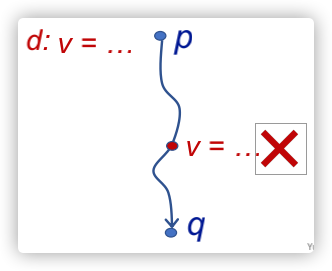
可达定义分析的一个应用场景:可以用于检测可能未初始化的变量;例如,在CFG的Entry节点,为所有的变量引入dummy definition(也就是代表未初始化变量的定义),如果dummy定义可到达点p,且定义对应的变量被使用,则这个点可能存在undefined错误;
前面说明过了数据流分析概念,那么根据其概念主要分三个步骤进行数据流分析:
- 明确Data Flow Values/Facts;
- 明确Transfer Function;
- 明确Control Flow Handing;
需要注意的是,可达定义分析使用的是forward analysis;
(1)明确Data Flow Values/Facts
对于可达定义分析而言,我们需要关联的Data Flow Values或者说Facts,是程序中所有变量的定义,每个定义可以使用一个bit进行表示,图示如下:
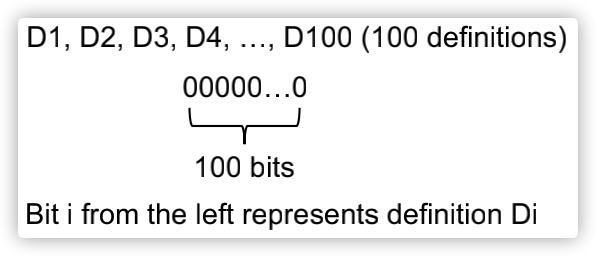
(2)明确Transfer Function
例如存在如下statement:
| |
这是一个很简单的赋值语句,也就是给变量v进行定义(赋值)。在这个statement中,生成了一个定义D,并且杀死(kill)了程序中所有其他的对v的定义,同时不影响这个statement中其他变量的定义;
由此transfer functions的公式可以表示为:
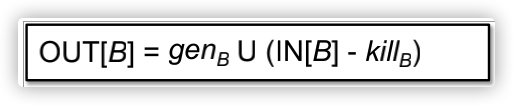
含义很简单,新生成的定义为genB,IN[B]-killB指的是进入当前BB的定义减去被杀死(重新定义)的定义,两者进行并操作,就是最终从这个BB流出的定义;
一个例子如下,需要注意的是,kill时需要kill掉所有其他BB的定义,即使这个BB是当前BB之前的:
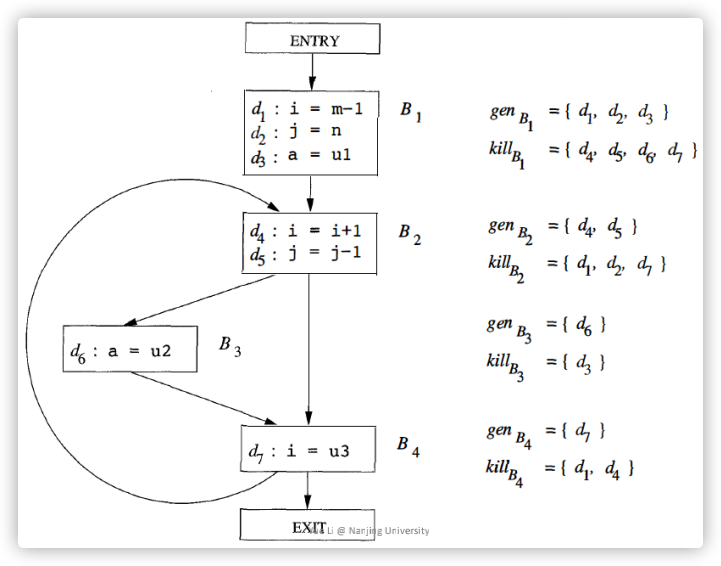
(3)明确Control Flow Handing
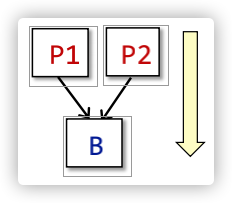
同理,对于merges处,可以很简单得到Control Flow的公式如下:

merge图示如下:
最后就可以得到可达定值分析的算法了,如下所示:

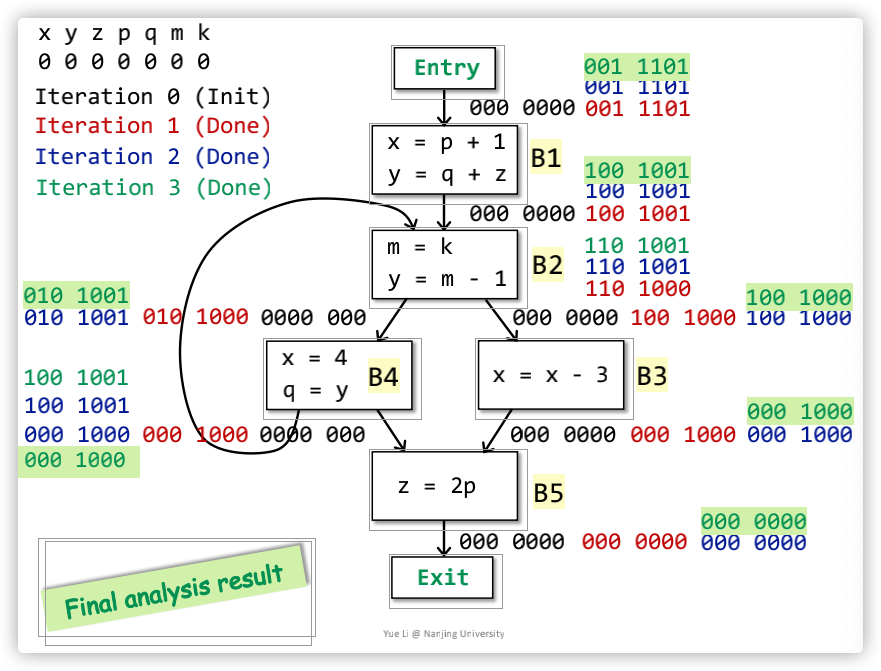
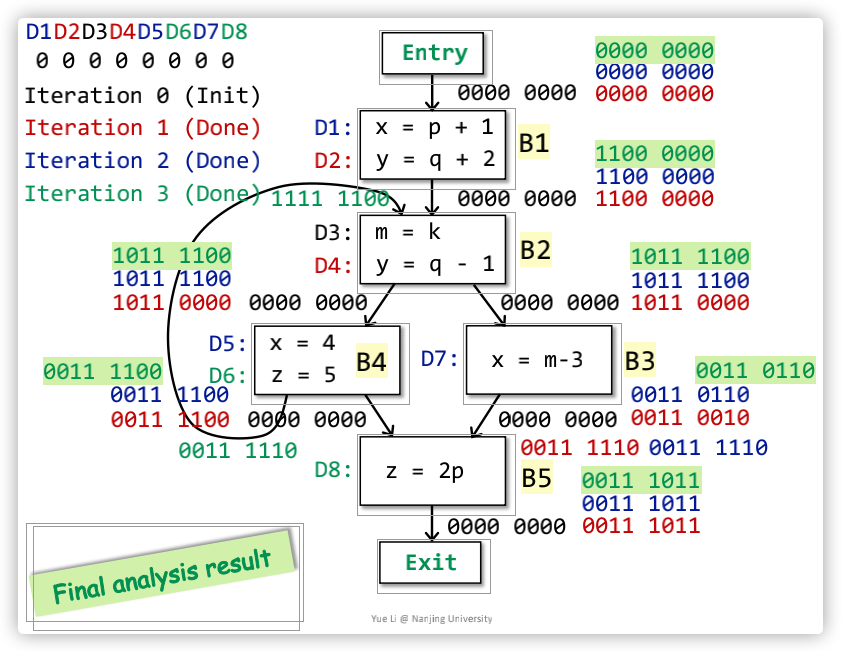
一个计算案例如下,只贴出了最终的一个计算结果,不过也可以很简单的知道中间的演算过程的(bits使用了不同颜色标记,每种颜色就是一次迭代演算):
Live Variables Analysis
即存活变量分析,变量存活分析告诉我们,变量v在程序点p是否可用,如果可用,则说变量v存活,反之亦反;也就是如果变量v在位置p存活,意味着从p点到程序结束,变量v可能会被用到,反之亦反;同时变量存活还包含一个隐含的含义:变量v在使用之前不能被redefined;图示如下:

针对变量存活分析,使用同样的套路分三步走,只不过变量存活使用backward analysis:
(1)明确Data Flow Values/Facts
对于变量存活分析,我们关注的抽象数据就是程序中的所有变量,仍然可以使用bit来进行表示,如下图所示:
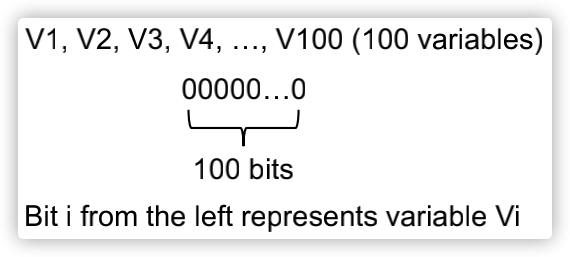
(2)明确Transfer Function
例如如下图示:
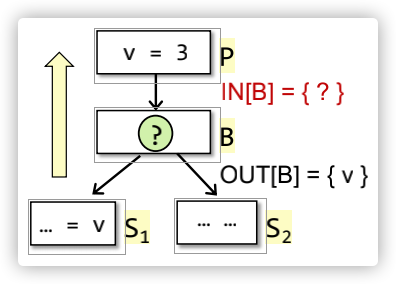
使用backward analysis可以得到Transfer functions公式如下:

(3)明确Control Flow Handing
公式如下:
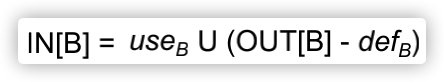
一个帮助理解的图示如下:
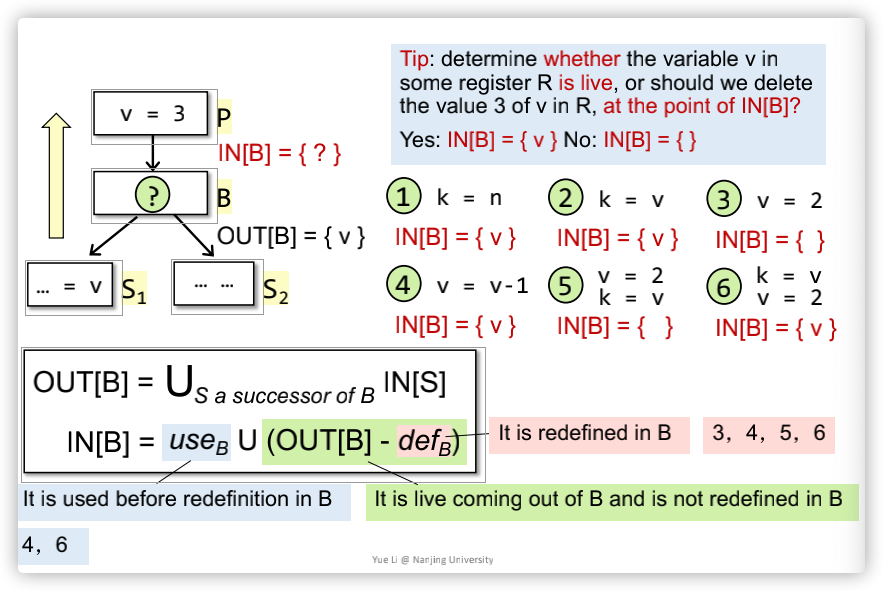
最终的算法如下:

一个演算案例如下: