什么是树

树是一种类似于链表的数据结构，不过链表的节点是以线性方式简单的指向其后继节点，而树的一个节点可以指向许多个节点。树是一种典型的 非线性 结构。

对于树ADT（抽象数据类型），元素的顺序不是考虑的重点。 如果需要用到元素的顺序信息，那么可以使用链表、队列、栈等线性数据结构 。

术语

图示

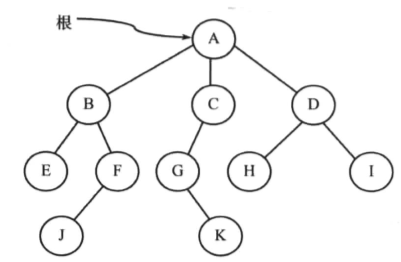
  • 根节点：根节点是一个没有双亲节点的节点。 一棵树中最多有一个根节点 。（上图的A节点就是根节点）。
  • 边：边表示从双亲节点到孩子节点的链接（如上图中所有的链接）。
  • 叶子节点：没有孩子节点的节点叫做叶子节点（如E、J、K、H和I）。
  • 兄弟节点：拥有相同双亲节点的所有孩子节点叫做兄弟节点（B、C、D彼此之间是兄弟节点）。
  • 祖先节点：如果存在一条从根节点到节点q的路径，且节点p出现在这条路径上，那么就可以把节点p叫做节点q的祖先节点，节点q也叫做p的子孙节点（A、C、G是K的祖先节点）。
  • 节点的大小：节点的大小是指子孙的个数， 包括其自身 （节点C的大小为3）。
  • 树的层：位于相同深度的所有节点的集合叫做树的层（B、C、D具有相同的层）。 根节点位于0层 。
![树的层][p1]
  • 节点的深度：从根节点到该节点的路径长度（G点的深度为2，A-C-G）。
  • 节点的高度：是指从该节点到最深节点的路径长度。 树的高度是指从根节点到树中最深节点的路径长度，只含有根节点的树的高度为0 （节点B的高度为2，B-F-J）。
  • 树的高度：是树中所有节点高度的最大值，树的深度是树中所有节点深度的最大值。对于同一棵树，其深度和高度是相同的。但是对于每一个节点，其深度和高度不一定相同。
  • 斜树：如果树中除了叶子节点外， 其余每个节点只有一个孩子节点 ，则这种节点称为斜树。对于每个节点只有一个左孩子节点的树称为左斜树。类似的，对于每个节点只有一个右孩子节点的树叫做右斜树。
![斜树][p2]

二叉树

如果一棵树中每个节点仅有0、1或者2个孩子节点，那么这棵树就称为 二叉树 。 空数也是一颗有效的二叉树 。一颗二叉树可以看做由根节点和两颗不相交的子树（分别称为左子树和右子树）组成，如下图所示：

![二叉树][p3]

二叉树的类型

  • 严格二叉树：二叉树中的每个节点要么有 两个 孩子节点，要么 没有 孩子节点。
![严格二叉树][p4]
  • 满二叉树：二叉树中的每个节点恰好有 两个 孩子节点且 所有的叶子节点都在同一层 。
![满二叉树][p5]
  • 完全二叉树：在定义完全二叉树之前，假设二叉树的高度为h。对于完全二叉树，如果将所有节点从根节点开始从上至下、从左到右，依次编号（假定根节点的编号为1），那么将得到从1~n（n为节点总数）的完整序列。在遍历过程中对于空指针也应该赋予编号。如果所有的叶子节点的深度为h或者h-1，且在节点编号序列中没有漏掉任何数字，那么这样的二叉树称为完全二叉树。
![完全二叉树][p6]

二叉树的性质

假设二叉树的高度的高度为h，且根节点的深度为0。那么二叉树的性质如下：

二叉树的性质

二叉树的结构

结构图示如下：

![二叉树图示][p8]

代码例子如下：

public class BinaryTreeNode{
	private int data;
	private BinaryTreeNode left;
	private BinaryTreeNode right;
	//getter and setter
}

Notice： 在树中，默认的流向是从双亲节点指向孩子节点，但并不强制表示为有向边。例如，如下两种表示方式是相同的：

![树的节点的两种表示方式][p9]

二叉树的操作

① 基本操作：

  • 向树中插入一个元素。
  • 从树中删除一个元素。
  • 查找一个元素。
  • 遍历树。

② 辅助操作：

  • 获取树的大小。
  • 获取树的高度。
  • 获取其最大的层。
  • 对于给定的两个或多个节点，找出他们的最近公共祖先（Least Common Ancestor，LCG）。

二叉树的应用

  • 编译器中表达式树。
  • 用于数据压缩算法中的和夫曼编码树。
  • 支持在集合中查找、插入和删除，其平均时间复杂度为O(logn)的二叉搜索（或称为查找）树（BST）。
  • 优先队列（PQ），它支持以对数时间（最坏情况下）对集合中的最小（或最大）数据单元进行搜索和删除。

二叉树的遍历

遍历的分类

二叉树遍历的分类

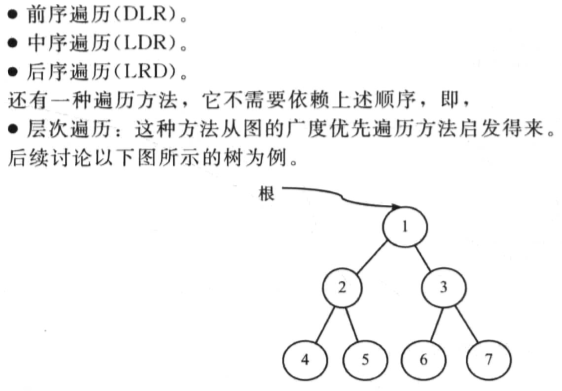
前序遍历

前序遍历一般规定先遍历左子树，然后遍历由子树。前序遍历的操作顺序如下：

  1. 访问根节点。
  2. 按照前序遍历方式遍历左子树。
  3. 按照前序遍历方式遍历右子树。

基于递归方式的前序遍历代码示例如下：

void preOrder(BinaryTreeNode root){
	if(root!=null){
		//先处理当前节点
		System.out.println(root.getData());
		//再处理左子树
		preOrder(root.getLeft());
		//最后处理右子树
		preOrder(root.getRight());
	}
}

基于迭代方式的前序遍历代码示例如下：

void preOrder(BinaryTreeNode root){
	if(root==null) return null;
	Stack<BinaryTreeNode> cache=new Stack<>();
	while(true){
		//先从根节点开始，将所有子树的根节点从高到低添加到栈内
		while(root!=null){
			//首先处理根节点（前序遍历首先处理根节点）
			System.out.println(root.get);
			cache.push(root);
			root=root.getLeft();
		}
		//如果栈内没有节点了
		if(cache.isEmpty()) break;
		//出栈，找到其右子树
		root=cache.pop().getRight();
	}
}

中序遍历

中序遍历的操作顺序如下：

  1. 按中序遍历方式遍历左子树。
  2. 访问根节点。
  3. 按中序遍历方式遍历右子树。

基于递归方式的中序遍历代码示例如下：

void inOrder(BinaryTreeNode root){
	if(root!=null){
		inOrder(root.getLeft());
		System.out.println(root.getData());
		inOrder(root.getRight());
	}
}

基于迭代方式的代码示例如下：

void inOrder(BinaryTreeNode root){
	if(root==null) return null;
	Stack<BinaryNode> cache=new Stack<>();
	while(true){
		while(root!=null){
			cache.push(root);
			root=root.getLeft();
		}
		if(cache.isEmpty()) break;
		root=root.pop();
		System.out.println(root.getData());
		root=root.getRight();
	}
}

后序遍历

后序遍历的操作顺序如下：

  1. 按后序遍历左子树。
  2. 按后序遍历右子树。
  3. 访问根节点。

基于递归方式的后序遍历代码示例如下：

void postOrder(BinaryTreeNode root){
	if(root!=null){
		postOrder(root.getLeft());
		postOrder(root.getRight());
		System.out.println(root.getData());
	}
}

基于迭代方式的后序遍历代码示例如下：

public List<Integer> postorderTraversal(TreeNode root){
    ArrayList<Integer> result = new ArrayList<>();
    if(root==null){
        return result;
    }
    Stack<TreeNode> cache = new Stack<>();
    cache.push(root);
    TreeNode lastPop=null;
    while(!cache.isEmpty()){
        while(cache.peek().left!=null){
            cache.push(cache.peek().left);
        }
        while(!cache.isEmpty()){
            if(cache.peek().right==null||cache.peek().right==lastPop){
                lastPop  = cache.pop();
                result.add(lastPop.val);
            }else if (cache.peek().right!=null){
                cache.push(cache.peek().right);
                break;
            }
        }
    }
    return result;
}

层次遍历

层次遍历的操作顺序如下：

  1. 访问根节点。
  2. 在访问第n层时，将n+1层的节点按顺序保存到队列中。
  3. 进入下一层并访问该层的所有节点。
  4. 重复上述操作直至所有层都访问完。

一个代码示例如下：

void levelOrder(BinaryTreeNode root){
	if(root==null) return;
	BinaryTreeNode temp;
	Queue<BinaryTreeNode> cache=new LinkedList<>();
	cache.offer(root);
	while(!cache.isEmpty){
		temp=cache.poll();
		BinaryTreeNode left=temp.getLeft();
		BinaryTreeNode right=temp.getRight();
		if(left!=null){
			cache.offer(left);
		}
		if(right!=null){
			cache.offer(right);
		}
	}
}

通用树(N叉树)

二叉树最多有2个孩子节点，这种树很容易就用两个指针表示。但是如果一棵树的每个节点可以有任意多个子节点，而且不知道一个节点到底有多少个子节点，如下图所示便是N叉树：

n叉树

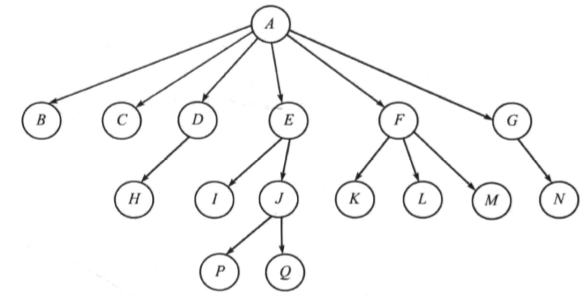
N叉树的表示

可以利用“第一个孩子/下一个兄弟”表示法，具体的步骤如下：

  1. 同一个双亲节点的孩子节点（兄弟节点）从左至右排列。
  2. 双亲节点只指向第一个孩子节点，删除从双亲节点到其他孩子节点的链接。

节点图示如下：

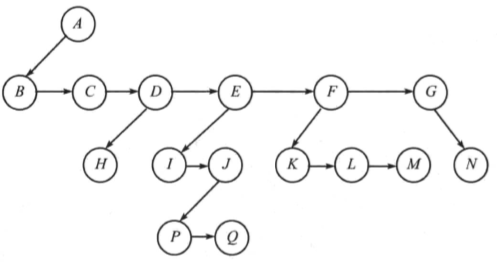
N叉树的表示

实际表示如下：

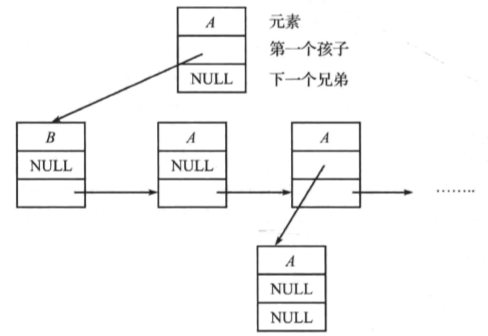
N叉树的实际表示

代码示例如下：

public class TreeNode{
	public int data;
	public TreeNode firstChild;
	public TreeNode nextSibing;
	// getter and setter...
}

N叉树的“孩子/兄弟”表示法理解

如果孩子节点之期存在一条链路相连，那么双亲节点就不需要额外的指针指向所有的孩子节点，因为从双亲节点的第一个孩子节点开始就可以遍历所有的元素，所以双亲节点用一个指针指向其第一个孩子节点，且同一个双亲节点的所有孩子节点之间都有链路，那么就能解决N叉树的表示问题。

线索二叉树

线索二叉树的分类

  • 如果只在空左指针存储前驱信息，则把这样的二叉树称为 左线索二叉树
  • 如果只在空右指针存储后继信息，则把这样的二叉树称为 右线索二叉树
  • 如果在空左指针存储前驱信息，并且在空右指针存储后继信息，则把这样的二叉树称为 满线索二叉树或者简单的称为线索二叉树

线索二叉树的分类

  • 前序线索二叉树：空左指针存储前序序列的前驱信息，空右指针存储前序序列后继信息。
  • 中序线索二叉树：空左指针存储中序序列的前驱信息，空右指针存储中序序列后继信息。
  • 后序线索二叉树：空左指针存储后序序列的前驱信息，空右指针存储后序序列后继信息。

线索二叉树结构

为了能够区分树的左右指针指向子节点还是线索，为此需要为每个节点添加两个附加字段，对于线索二叉树，节点的的形式如下图所示：

线索二叉树的结构

代码形式如下：

public class ThreadedBinaryTreeNode{
	public ThreadedBinaryTreeNode left,right;
	public bool lTag.rTag;
	// getter and setter
}

代码中的lTag和rTag的说明如下：

  1. 如果lTag为false，则代表左指针指向序列的前驱节点；lTag为true，则代表左指针指向左孩子节点。
  2. 如果rTag为false，则代表右指针指向序列的后继节点；rTag为true，则代表右指针指向右孩子节点。

下面给出一个中序线索二叉树的图示：

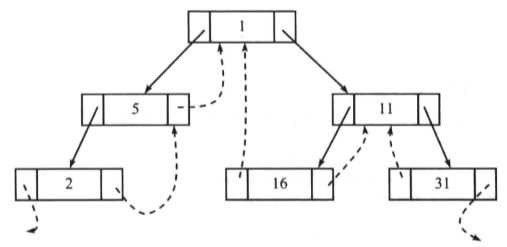
中序线索二叉树

线索二叉树的一个技巧

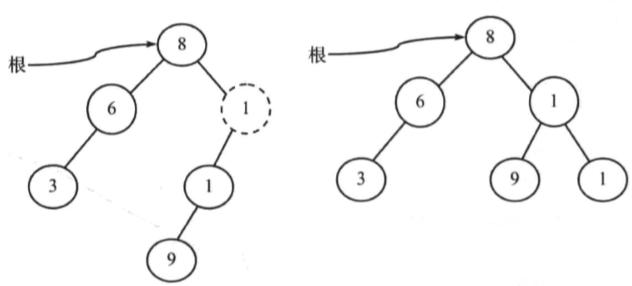
在线索二叉树的表示中，一个通常的约定是使用一个特定的哑结点，对于空树也是如此。哑结点的右标签是1，且右指针指向其自身。图示如下：

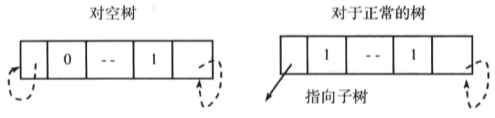
线索二叉树的哑结点

表达式树

  1. 用来表示表达式的树叫做 表达式树 。
  2. 在表达式树中，叶子节点是操作数，而非叶子节点是操作符。
  3. 表达式树由二元表达式组成，对于一元操作符，一个子树将为空。

下图为表达式(A+B*C)/D对应的一个简单表达式树的图示：

表达式树

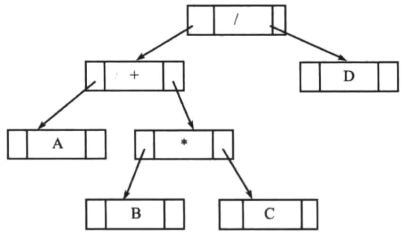
基于后缀表达式构建表达式树

思路

  1. 每次读入一个符号，如果是操作数，就创建一个节点，并把指向该节点的指针入栈。
  2. 如果该符号是操作符，则从栈中弹出两个指向树T1，T2的指针（其中T1先出栈）。
  3. 产生一颗新树，该树的根节点为读到的操作符，T1为其左孩子，T2为其右孩子。
  4. 将指向新产生的树的指针入栈。

例如后缀表达式：ABC*+D/ ，下面对其进行表达式树构建的图解：

  1. 产生三个节点，并将它们入栈：
    图解1

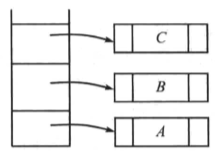
  2. 读入操作符“*”，因此栈中指向两棵树的指针出栈，并形成一颗新树，最后将指向新树的指针入栈：
    图解2

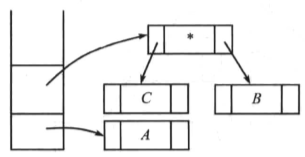
  3. 读入操作符“+”，因此将指向树的两个指针出栈，形成一颗新树，并将指向新树的指针入栈：
    图解3

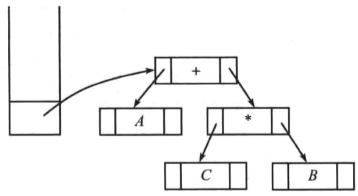
  4. 读入操作数“D”，产生包含一个节点的树。将指向该树的指针入栈：
    图解4

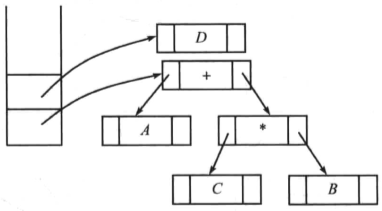
  5. 读入操作符“/”，将栈中指针所对应的两棵树合并，并将指向最后树的指针入栈：
    图解5

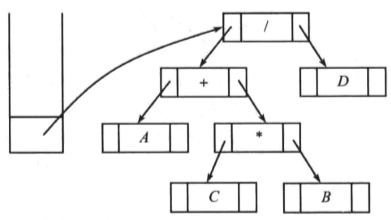
代码实现

BinaryTreeNode BuildExprTree(char[] input){
	Stack<Character> cache=new Stack<>();
	for(int i=0;i<input.length;i++){
		if(input[i].isDigit()){
			BinaryTreeNode newNode=new BinaryTreeNode();
			newNode.setData(input[i]);
			cache.push(newNode);
		}else{
			BinaryTreeNode t2=cache.pop();
			BinaryTreeNode t1=cache.pop();
			BinaryTreeNode newNode=new BinaryTeeNode();
			newNode.setData(input[i]);
			newNode.setLeft(t1);
			newNode.setRight(t2);
			cache.push(newNode);
		}
	}
	return cache.pop();
}

二叉搜索树

为什么使用二叉搜索树(BST)

对于普通的二叉树，在最坏的情况下，搜索的时间复杂度为O(n)，但是如果使用BST，那么可以使得在最坏的情况下平均搜索的时间复杂度降低到O(logn)。

BST的性质

  • 一个节点的左子树只能包含键值小于该节点键值的节点。
  • 一个节点的右子树只能包含键值大于该节点键值的节点。
  • 左子树和右子树也必须是二叉搜索树。

Notice： 树中的每个节点都要满足这个性质。

例如如下图中右边的二叉树便不是二叉搜索树（2比3小）：

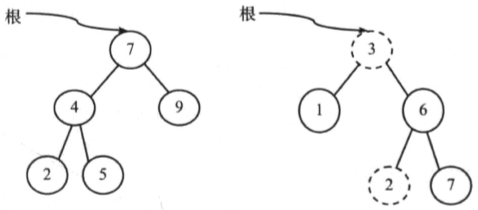
二叉搜索树

BST的注意事项

  1. 由于根节点数据总是处于左子树和右子树数据之前，所以当中序遍历二叉搜索树时，将得到一个有序表。
  2. 搜索一个元素时，如果根节点数据小于要搜索的元素，则跳过根节点的左子树；同样，如果根节点数据大于要查找的元素，则跳过根节点的右子树。总而言之： 二叉搜索树要么在左子树中搜索，要么在右子树中搜索，不需要同时在两个数中搜索 。

在二叉搜索树中寻找元素

递归版本代码示例如下：

BSTNode find(BSTNode root,int target){
	if(root==null){ return null; }
	if(target<root.getData()){
		return find(root.getLeft(),target);
	}else if(target>root.getData()){
		return find(root.getRight(),target);
	}
	return root;
}

非递归版本代码示例如下：

BSTNode find(BSTNode root,int target){
	if(root==null){ return null; }
	while(root!=null){
		if(target==root.getData()){
			return root;
		}else if(target>root.getData()){
			root=root.getRight();
		}else{
			root=root.getLeft();
		}
	}
	return null;
}

在BST中寻找最小元素

在BST中，最左边的为最小元素，它没有左子节点。根据这个特点得出如下两种代码写法：

递归版本的代码示例如下：

BSTNode findMin(BSTNode root){
	if(root==null){ return null; }
	if(root.getLeft()==null){
		return root;
	}else{
		return findMin(root.getLeft());
	}
}

非递归版本如下：

BSTNode findMin(BSTNode root){
	if(root==null){ return null; }
	while(root.getLeft()!=null){
		root=root.getLeft();
	}
	return root;
}

在BST中寻找最大元素

在BST中，最大元素在树的最右端，他没有右节点。根据这个特点得出如下两种代码写法：

递归版本的代码示例如下：

BSTNode findMax(BSTNode root){
	if(root==null){ return null; }
	if(root.getRight()==null){
		return root;
	}else{
		return findMax(root.getRight());
	}
}

非递归版本代码示例如下：

BSTNode findMax(BSTNode root){
	if(root==null){ return null; }
	while(root.getRight()!=null){
		root=root.getRight();
	}
	return root;
}

寻找中序序列前驱和后继

如果X节点有两个孩子节点，那么中序序列前驱为其左子树中值最大的元素，而其后继为其右子树中最小的元素。图示如下：

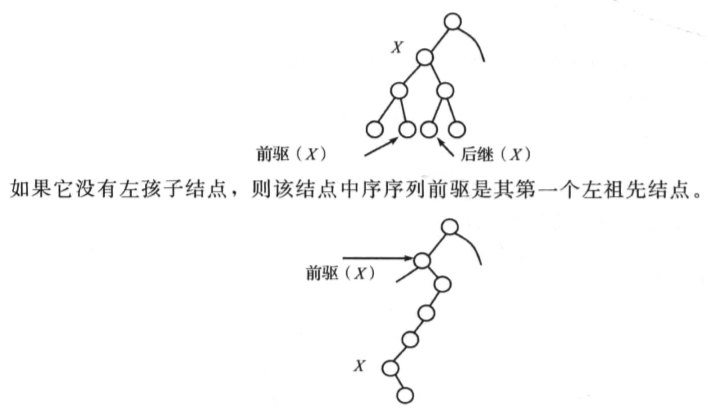
BST中序序列前驱和后继

在BST中插入元素

一个代码示例如下：

BSTNode insert(BSTNode root,int data){
	if(root==null){
		root=new BSTNode();
		root.setData(data);
	}else{
		if(data<root.getData()){
			root.setLeft(insert(root.getLeft(),data));
		}else if(data>root.getData()){
			root.setRight(insert(root.getRight(),data));
		}
	}
	return root;
}

在BST中删除元素

一个代码示例如下：

BSTNode delete(BSTNode root,int data){
	BSTNode temp;
	if(root==null){
		return null;
	}else if(data<root.getData()){
		root.setLeft(delete(root.getLeft(),data));
	}else if(data>root.getData()){
		root.setRight(delete(root.getRight(),data));
	}else{
		//如果找到该元素了
		//如果被删除节点存在左右子树
		if(root.getLeft()!=null&&root.getRight()!=null){
			temp=findMax(root.getLeft());
			root.setData(temp.getData());
			root.setLeft(delete(root.getLeft(),root.getData()));
		}else{
			//如果不能存在孩子节点
			if(root.getLeft()==null&&root.getRight()==null){
				root=null;
			}else if(root.getLeft()==null){
				//如果存在右孩子节点
				root=root.getRight();
			}else if(root.getRight()==null){
				//如果存在左孩子节点
				root=root.getLeft();
			}
		}
	}
	return root;
}

平衡二叉搜索树

通常，高度平衡树用符号HB(k)表示，其中k为左子树和右子树的高度差。有时也把k叫做平衡因子。

完全平衡二叉树

在HB(k)中，如果k=0，那么就把这种二叉树叫做完全平衡二叉树。即，在HB(0)的二叉搜索树中，左子树和右子树的高度差最多为0。这就能够保证树为完全二叉树。例如下图：

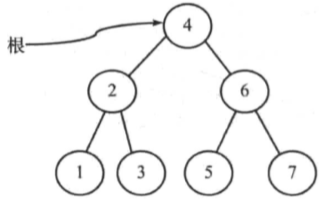
完全平衡二叉树

AVL树

在HB(k)中，如果k=1，那么这种的二叉搜索树叫做AVL树。即一个AVL树是带有平衡条件的二叉搜索树：左子树和右子树的高度差最多不能超过1。

AVL树的性质

  • 它是一颗二叉搜索树。
  • 对任意节点X，其左子树的高度与其右子树的高度的差最多不超过1。

例如下图中，左边的树不是AVL树，而右边的是AVL树：

AVL树图示

旋转

旋转是用来保持AVL树性质的技术。即，需要在节点X应用旋转操作。如果在AVL树中插入一个节点，那么我们需要修复这个AVL树（保证插入后整个树任然满足AVL的性质），我们只需要关注从插入点到根节点路径上的第一个不满足AVL性质的节点，并修复它。

违背AVL树性质的类型

  • 在节点X的左孩子节点的左子树中插入元素（LL型）。
  • 在节点X的左孩子节点的右子树中插入元素（LR型）。
  • 在节点X的右孩子节点的左子树中插入元素（RL型）。
  • 在节点X的右孩子节点的右子树中插入元素（RR型）。

第1种情况和第4中情况是对称的，很容易由单旋转来解决。类似的，第2种情况和第3种，需要双旋转才能解决（需要两个单旋转）。

单旋转

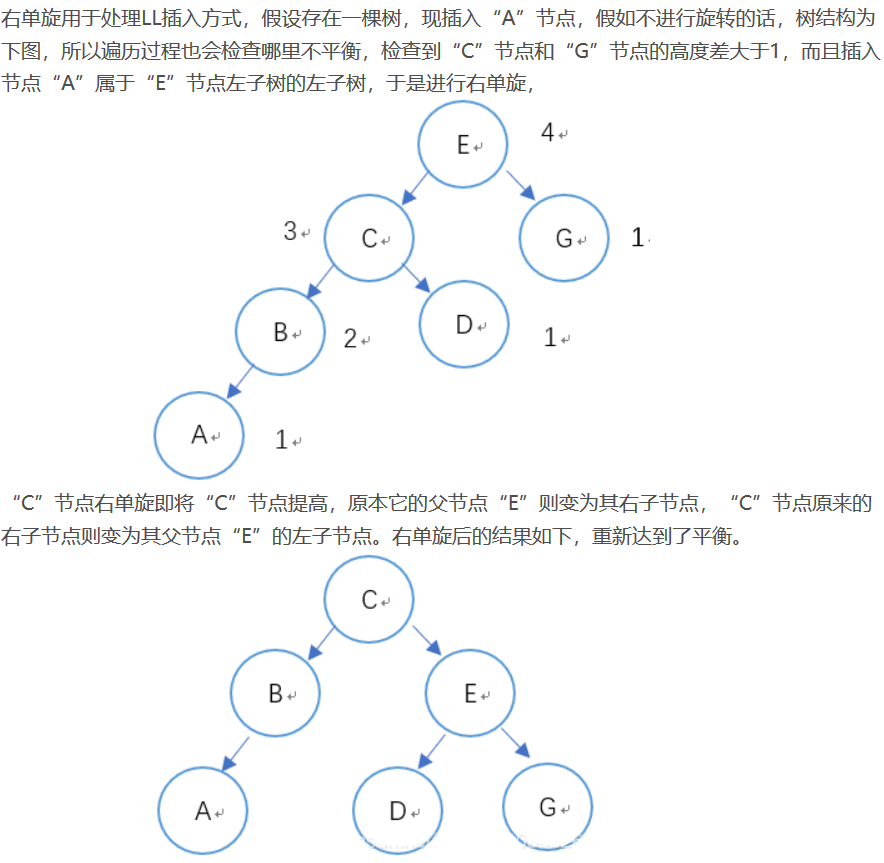
右单旋

右单旋用于处理LL型插入方式。一个图解如下：

右单旋图解

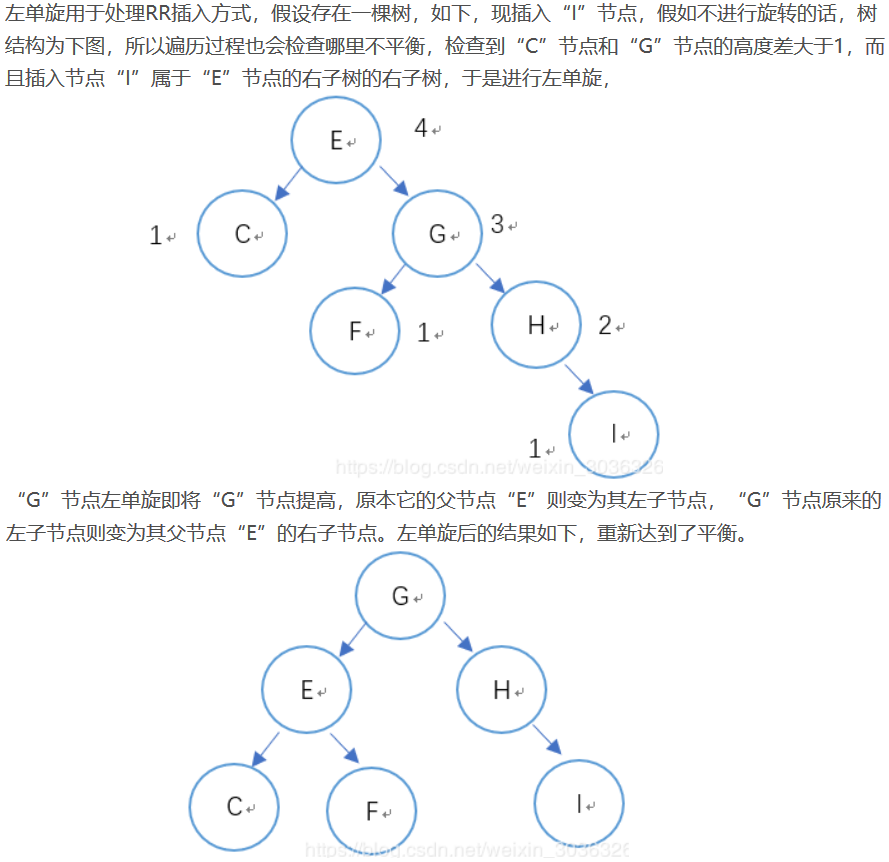
左单旋

左单旋用于处理RR型插入方式。一个图解如下：

左单旋图解

双旋

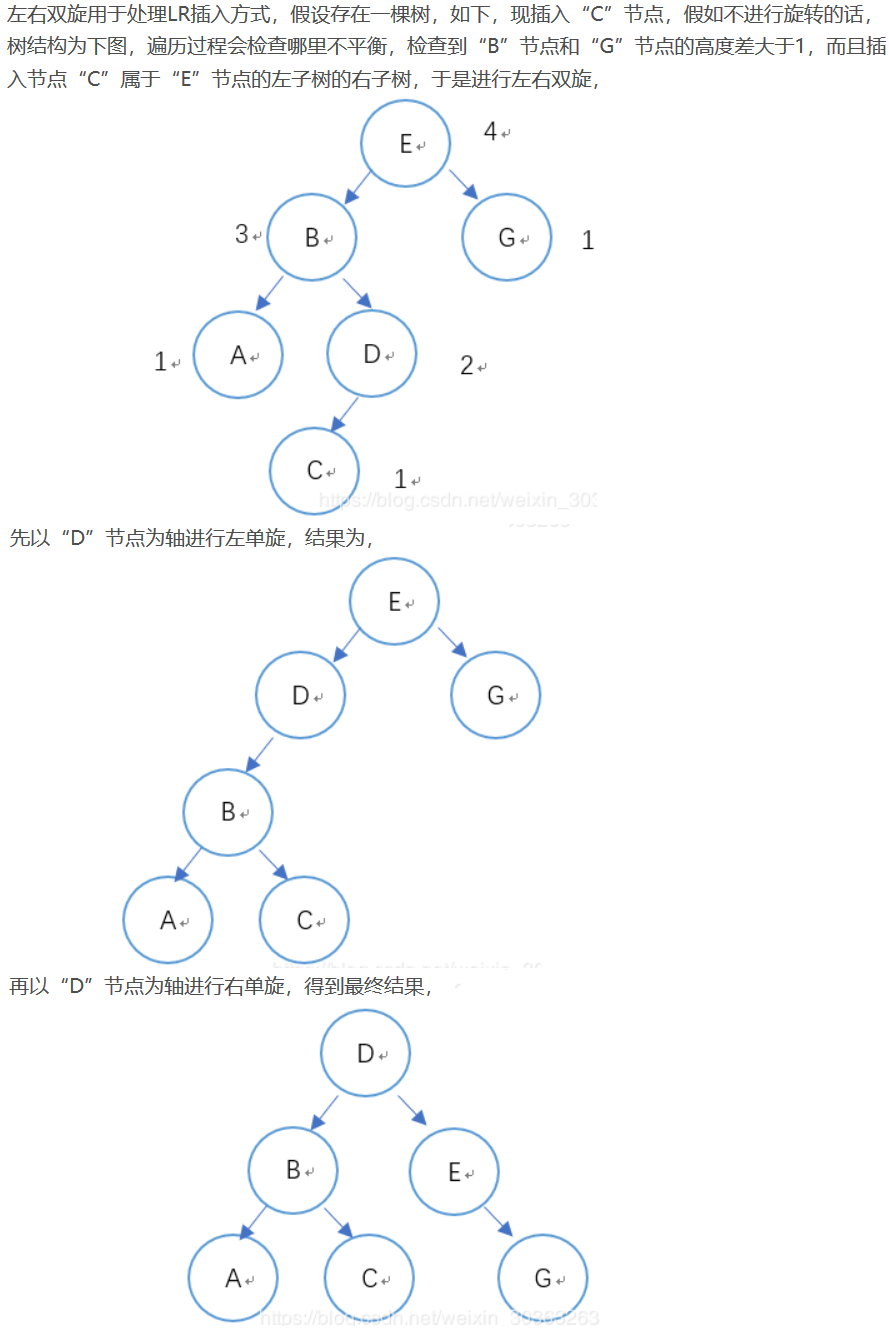
左右双旋

左右双旋用于处理LR插入方式。一个图解如下：

左右双旋图解

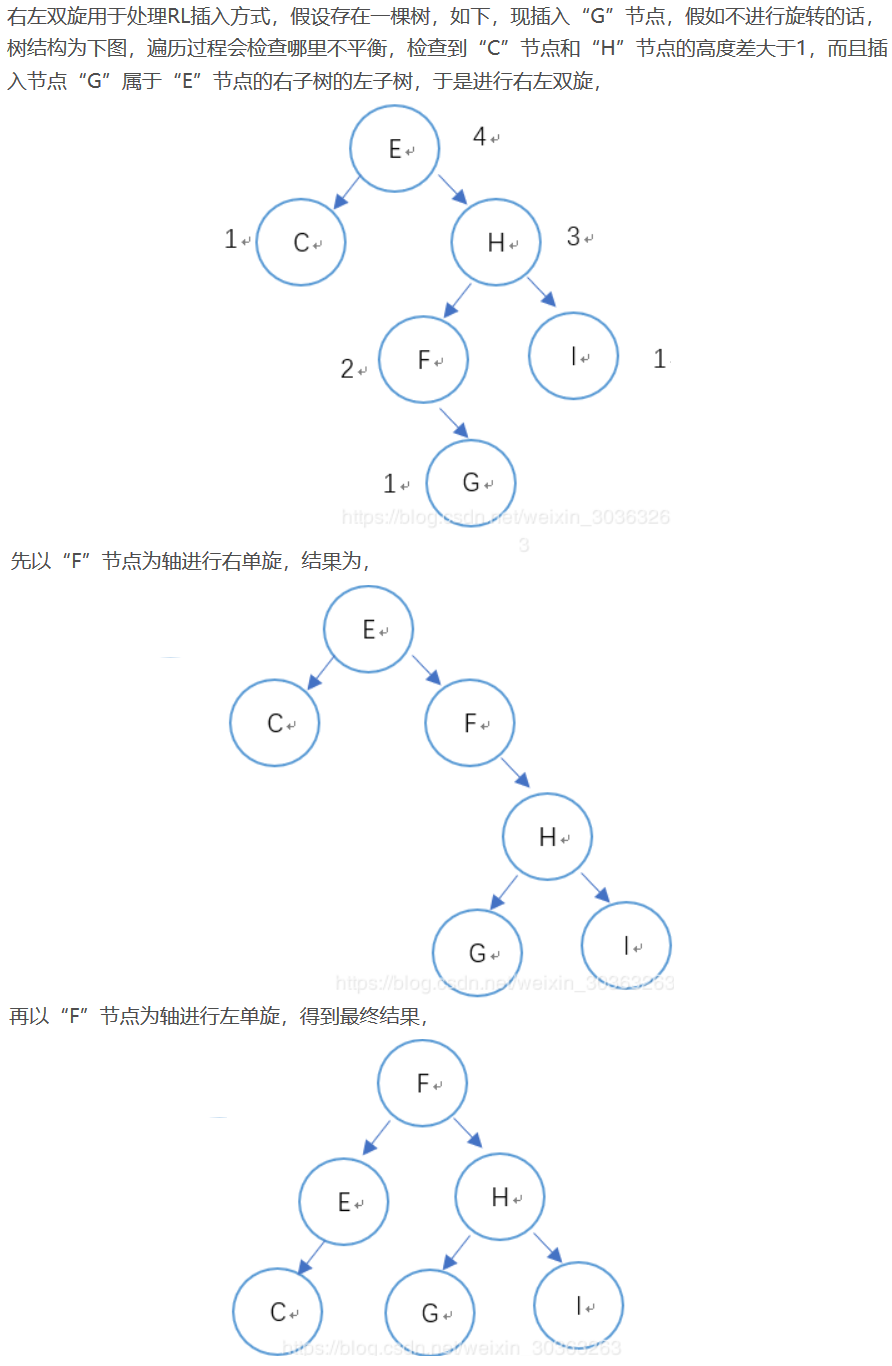
右左双旋

右左双旋用于处理RL型插入。一个图解如下：

右左双旋图解